3.1.1 Cinemática
Existen dos problemas fundamentales para resolver la cinemática del robot, el primero de ellos se conoce como cinemática directa, y consiste en determinar cuál es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia, conocidos los valores de las articulaciones y los parámetros geométricos de los elementos del robot. El segundo denominada cinemática inversa resuelve la configuración que debe adoptar el robot para una posición y orientación del extremo conocidas.
3.1.1.1 Cinemática Directa
Denavit y Hartenberg propusieron un método sistemático para descubrir y representar la geometría espacial de los elementos de una cadena cinemática (ver Tabla 3-1), y en particular de un robot, con respecto a un sistema de referencia fijo [25]. Este método utiliza una matriz de transformación homogénea para descubrir la relación espacial entre dos elementos rígidos adyacentes, la cinemática directa consiste en encontrar una matriz de transformación homogénea 4 X 4 que relacione la localización espacial del robot con respecto al sistema de coordenadas de su base (ver Figura 3.1 ).
El origen se toma en la cadera del robot, como se observa el eje Z está orientado
perpendicularmente al eje X. Con esto, entonces se obtiene la matriz de transformación
homogénea.
Como se puede observar en la última columna la matriz de (ec. 3.3) la transformación
homogénea nos da la cinemática directa.
3.1.1.2 Cinemática Inversa
El objetivo de la cinemática inversa consiste en encontrar el ángulo que deben adoptar las diferentes articulaciones para que el final del sistema articulado llegue a una posición concreta [6]. Como se muestra en la Figura 3.3, dadas las características de las longitudes del fémur y de la tibia, la cinemática inversa solo se definirá a partir del vector de posición del punto final del efector (Px, Py). Para este caso en particular no se llevaron a cabo las simulaciones debido a que solamente se tienen dos ángulos y por consiguiente solamente se dejan plasmadas las ecuaciones.
Retomando la ecuación 3.4, se despejarán las incógnitas, en este caso son θ1 y θ2. Cuando se obtiene una solución, puede que resulte más de una solución para llegar al resultado.
Así, para encontrar θ2, tenemos:
Simplificando:
Para encontrar θ1, despejamos la incógnita que tenemos en la ecuación 3.4, queda de la siguiente forma:
El resultado de la cinemática inversa son las ecuaciones 3.8 y 3.17, con éstas, se puede corroborar el resultado mostrado en la cinemática directa.
Fuente:
TESIS DE MAESTRÍA EN CIENCIAS
“Construcción de un Robot Bípedo Basado en Caminado
Dinámico”
Presentada por:
Ing. Cesar Humberto Guzmán Valdivia
Ing. en Mecatrónica por la Universidad Politécnica de Zacatecas.
Gracias por el interés.




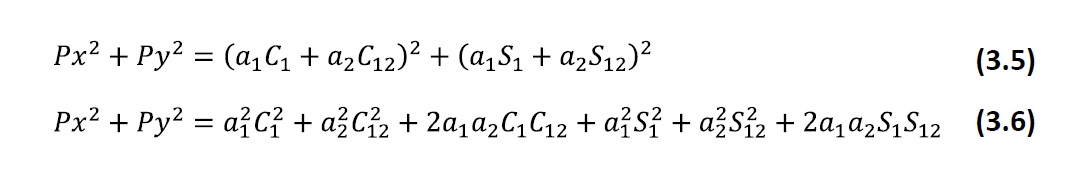


No hay comentarios:
Publicar un comentario